Video: Er de to diagonalene til et parallellogram like?
2024 Forfatter: Lynn Donovan | [email protected]. Sist endret: 2023-12-15 23:51
Når en parallellogram er delt inn i to trekanter får vi se at vinklene på tvers av fellessiden(her diagonal ) er lik . Dette beviser at de motsatte vinklene i a parallellogram er også lik . De diagonaler til et parallellogram er ikke av lik lengde.
Bare så, er diagonaler til et parallellogram kongruente?
Alle egenskapene til en parallellogram gjelder (de som betyr noe her er parallelle sider, motsatte sider er det kongruent , og diagonaler dele hverandre). Alle vinkler er per definisjon rette vinkler. De diagonaler er kongruent.
Man kan også spørre hvorfor diagonalene til et parallellogram ikke er kongruente? De diagonaler til et parallellogram er ikke lik. Fordi det parallellogram har tilstøtende vinkler som spisse og stumpe, den diagonaler del figuren i 2 par kongruent trekanter. Siden vinklene er spisse eller stumpe, er to av de kortere sidene av trekantene, både spisse og stumpe kongruent.
På samme måte, hva er diagonalen til et parallellogram?
Diagonal av Parallelogram Formel A parallellogram er en firkant hvis motsatte sider er parallelle og like. De motsatte sidene er parallelle og like, danner like vinkler på de motsatte sidene. Diagonaler til en parallellogram er segmentene som forbinder de motsatte hjørnene av figuren.
Er de to diagonalene til et rektangel like Hvorfor?
De to diagonaler er kongruente (samme lengde). Hver diagonal halverer den andre. Med andre ord, punktet hvor diagonaler krysse (kryss), deler hver diagonal inn i to like deler. Hver diagonal deler opp rektangel inn i to kongruente rettvinklede trekanter.
Anbefalt:
Er definert som forholdet mellom egenskapene til et objekt og egenskapene til en agent som gir ledetråder til bruken av et objekt?
En affordance er et forhold mellom egenskapene til et objekt og egenskapene til agenten som bestemmer hvordan objektet muligens kan brukes
Hvilket verktøy kan brukes til å legge til pakker til et frakoblet Windows 10-bilde?
Deployment Image Servicing and Management (DISM.exe) er et kommandolinjeverktøy som brukes til å oppdatere offline Windows®-bilder
Halver diagonaler alltid hverandre i et parallellogram?
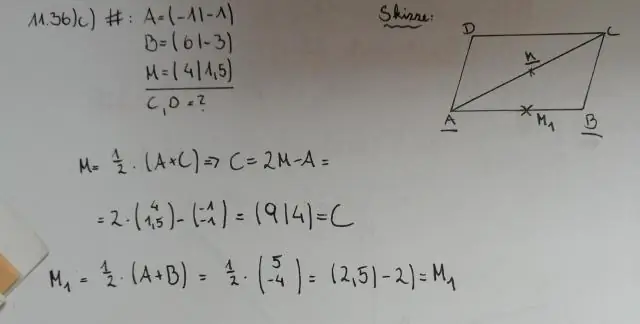
I ethvert parallellogram halverer diagonalene (linjer som forbinder motsatte hjørner) hverandre. Det vil si at hver diagonal kutter den andre i to like deler. I figuren ovenfor drar du et hvilket som helst toppunkt for å omforme parallellogrammet og overbevise deg selv om at det er slik
Halver diagonalene til parallellogrammet hverandre ved 90?
I enhver rombe halverer diagonalene (linjer som forbinder motsatte hjørner) hverandre i rette vinkler (90°). Det vil si at hver diagonal kutter den andre i to like deler, og vinkelen der de krysser er alltid 90 grader
Hvordan beviser du at diagonalene til en rombe deler hverandre?
I en rombe er alle sider like og motsatte sider er parallelle. Videre er en rombe også et parallellgram og viser derfor egenskapene til et parallellogram og at diagonalene til et parallellogram halverer hverandre